-" La matemáticas nos ayudan a descubrir la lógica que subyace al mundo tan complejo y caótico en el que vivimos " .- ....
..." si estuvieran entrevistándome desde la otra punta del Universo, nuestra biología podría ser distinta y nuestra química, incluso la física, pero creo que las matemáticas serían exactamente las mismas".....
Marcos du Santoy.
Catedrático de Matemáticas de la Universidad de Oxfor.
Obras:
La música de los número primos.
Simetría. Un viaje por los patrones de la Naturaleza.
Para los matemáticos es común emparentar la belleza de las matemáticas con la música y la poesía.
Bertrand Russel las define.-" Las matemáticas poseen no solo la verdad sino la belleza suprema, una belleza fría y austera, como una escultura sin apelación a ninguna parte de nuestra naturaleza débil, sin la hermosura de la pintura o la música, pero sublime y pura, y capaz de una perfección como solo las mejores artes pueden presentar. El verdadero espíritu del deleite, de exaltación, el sentido del ser más grande que el hombre puede encontrar tanto en la matemática como en la poesía ".-Algunos títulos de su prolifera obra:
Los principios de las Matemáticas.
Introducción a la filosofía matemática.
Un pensamiento suyo:
El problema de la humanidad es, que los estúpidos están seguros de todo, y los inteligentes están llenos de dudas.
Paul Erdos comentó:- " ¿ Por qué son bellos los números ?.
Es como preguntar, por qué es bella la novena sinfonía de Beethoven. Si no lo ves por qué, nadie te lo puede decir.
Yo se que los números son bellos. Si no lo son, entonces nada lo es ".-
Matemático húngaro ( 1.913- 1.996 )
Sus prolíferos trabajos sobre:
Combinatoria.
Toría de conjuntos y probabilidades.
etc.
**********************
La vida dura un instante, suficiente para hacer cosas eternas.
***********************
Cumbia Matemática
Cumbia Matemática
Nuestro entorno físico y conceptual tiene un alto nivel de complejidad.
Para abordar sus estudios necesitamos modelar la realidad extrayendo aquellos parámetros que sean significativos para su análisis, y que sean suficientes para obtener conclusiones.
Conseguido estos patrones, por medio de cálculos de razones, proporciones, etc. y analizados se llega a ....
Para abordar sus estudios necesitamos modelar la realidad extrayendo aquellos parámetros que sean significativos para su análisis, y que sean suficientes para obtener conclusiones.
Conseguido estos patrones, por medio de cálculos de razones, proporciones, etc. y analizados se llega a ....
LA BELLEZA DE LAS MATEMÁTICAS
***********************************
***********************************
EL NÚMERO DE ORO.-
Es un - NÚMERO IRRACIONAL INIMAGINABLE - que se encuentra desde siempre ligado a la estructura de la naturaleza de todo lo existente, NUESTRO MUNDO, GALAXIAS; y en los cálculos de la belleza, ARTE Y DISEÑO, desde la época griega, y quizás, antes en otras culturas.Es llamado el NÚMERO DE ORO, PROPORCIÓN ÁUREA, RAZÓN ÁUREA, O PROPORCIÓN DIVINA.
En la antigüedad le asociaban a los dioses, por ser la EXPLICACIÓN MATEMÁTICA, DE LA BELLEZA del arte, y de la naturaleza.
Una obra humana hecha con la proporción marcada por el número áureo, transmite a quien la observa una sensación de belleza y armonía.
El valor numérico es 1, 618.........., es un número irracional con infinitas cifras decimales sin que exista una secuencia de repetición para que sea un número decimal periódico.
Al número de oro 1,618.......... se le denomina ( Fi ), que es la inicial del nombre
del escultor griego constructor del Partenón, Fídias, que le utilizó en sus trabajos.
La proporción áurea la tienen presente los pintores afamados , y también en la naturaleza está presente en el reino vegetal, animal, y el universo.
ALGUNAS APLICACIONES.-
En el arte:
a ) - En determinada - PROPORCIÓN ENTRE SEGMENTOS-.
b ) - En el llamado - RECTÁNGULO DE ORO -.
c ) - En otras figuras geométricas como - EL PENTÁGONO -
Etc.
Y en la naturaleza le encontramos a traves de :
d ) -La - SUCESIÓN DE FIBONACCI-. etc.
e ) -Breve referencia al ANGULO DE ORO y la SIMETRÍA.
Breve referencia a los casos eunumerados.
a ) -Número de oro en la PROPORCIONALIDAD DE SEGMENTOS.-
Dado un segmento ab, se dice que está en proporción áurea, cuando la proporción entre el todo y la grande es la misma que entre la grande y la pequeña.Resolviendo la ecuación de segundo grado da,
También se puede expresar.
El segmento menor es al segmento mayor; como este es a la totalidad.
En los anillos de Saturno está presente la proporció áurea entre segmentos.
b ) - Proporción áurea en EL RECTÁNGULO DE ORO.
Para obtener el número áureo en un cuadrado, se traza un arco que tenga por centro el punto medio de uno de sus lados y su diámetro alcance el vértice del lado opuesto, desde ese punto se lleva el arco hasta su intercesión con la prolongación del lado elegido obteniéndose un segmento que llamamos Phi.
La relación entre Phi y un lado del cuadrado es el número áureo.
Este rectángulo con las proporciones perfectas, tiene la particularidad, que si le quitas un cuadrado, la parte restante vuelve a tener las proporciones perfectas y así indefinidamente.
Si el lado del cuadrado vale 2 unidades, es claro que el lado mayor del rectángulo
vale 1 + raíz cuadrada de 5., por lo que la proporción entre los lados es
= 1,61803 número de oro.
Utilizado en arquitectura, ( Partenón Pirámides egipcias ).
El Partenón ( mujer joven, virgen ), templo dórico situado en la Acrópolis de Atenas, fue mandado construir por Pericles en honor a la diosa Atenea y fue construido por Fídias.
Detalle y reconstrucción.-
En la pirámide Keops egipcia, anterior al Partenón, tiene el número de oro en su estructura.
Aida, Marcha Triunfal-----Verdi
El Templo de Ceres.-
Tiene su fachada construida siguiendo un sistema de triángulos áureos, relacionados con el orden dórico.
Dibujo de Leonardo da Vinci.
Las relaciones entre las distintas partes de un cuerpo humano perfecto, son proporciones áureas.
Leonardo da Vinci las plasmó en un celebre dibujo, en el que estirando manos y pies y haciendo centro en el ombligo se dibuja la circunferencia.
El cuadrado tiene por lado la altura del cuerpo que coincide con un cuerpo armonioso, con la longitud entre los extremos de ambas manos cuando los brazos están extendidos y forman un ángulo de 90 grados con el tronco.
Resulta que el cociente entre la altura del hombre ( lado del cuadrado ) y la distancia del ombligo a la punta de la mano ( radio de la circunferencia ) es el número áureo.
También está, entre la altura de la cadera y la rodilla, entre la falange de los dedos, la longitud de la cabeza y su anchura y en más partes de nuestra anatomía.
El famoso cuadro de Salvador Dalí Leda Atomic, la figura de Gala está pintada teniendo en cuenta la proporción áurea. 
La TORRE EIFFEL guarda la proporción del numero de oro Phi.
Los ejes de sus cuatro pilares forman un cuadrado de 100 metros, que sería el lado pequeño del rectángulo áureo.
Poniendo dos rectángulos conseguimos la altura de la torre.
100 x 2 x numero áureo 1.61805 = 323, 61 metros.
También se aplica el número de oro en el diseño,
tarjetas de crédito, carnets de identidad, cajetillas de tabaco etc.
c ) - Número de oro en EL PENTÁGONO.
La relación entre la diagonal del pentágono regular y su lado es el número de oro.
d ) - Número de oro en la SUCESIÓN FIBONACCI.
Formemos la siguiente sucesión de números:
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,..........
Cada término se forma con la suma de los dos anteriores.
La serie Fibonacci, fue descubierta por matemáticos hindúes y traída a Europa por Fibonacci.
Fibonacci, es el sobrenombre con que se le conoció al rico comerciante Leonardo de Pisa. (1.170 - 1.240 ).
Viajó por el norte de África y Asia y trajo a Europa algunos de los conocimientos matemáticos.
De la cultura árabe, la numeración, que se enfrentó a la romana.
De la cultura hindú, la famosa serie que tomo su nombre.
La propiedad más sorprendente de esta serie es; que al dividir dos términos sucesivos, siempre el mayor entre el menor vamos al encuentro del número de oro.
Sean los términos 89 y 55, dividiendo con seis decimales el resultado es 1.618182...., y más nos aproximamos entre más altos sean los términos elegidos; en la practica, con los decimales que se toman para trabajar resulta el número áureo.
Otras de sus curiosidades de esta sucesión es, que aparece en multitud de formas y fenómenos de la Naturaleza;
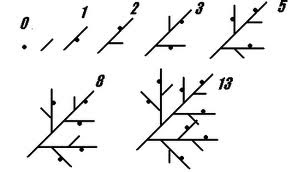
en los tallos de las plantas, en los pétalos de las flores, en las estrellas de mar, en las conchas de los caracoles..
En los Agujeros Negros y Galaxias.
El número de pétalos de una flor es generalmente un término de Fibonacci, 3,5,8,21,..... rara vez hay una que no se corresponda con una cifra de esta sucesión.
Esta serie de números son los favoritos de la Naturaleza y los hallamos por doquier en el mundo natural.
e ) - ANGULO DE ORO y la SIMETRIA -.
Si dividimos la circunsferencia de un circulo en dos porciones de manera que guarden la proporción áurea, cuyo planteamiento es:El total, es al segmento mayor, como el segmento mayor, es al menor.
El resultado es el angulo áureo que vale 137,5077º
Si el ÁNGULO ÁUREO lo representamos en un circulo repetidas veces, comprobamos que los puntos marcados se corresponde con la colocación que llevan a cabo en la naturaleza vegetal muchas plantas; hojas de una palmera, las escamas de una piña, las pipas en un girasol.
Nuestro mundo está cargado de geometría regular y de formas simétricas a todas las escalas y en todos los niveles relacionados con el número áureo.
El LENGUAJE MATEMÁTICO es:
el LENGUAJE DE LA BELLEZA, y se manifiesta desdes una molécula a una galaxia.
La SIMETRÍA ESTA EN EL CORAZÓN DE LA NATURALEZA, y para muchos es:EL LENGUAJE DE LA NATURALEZA, porque la simetria transmite información; es la forma de comunicarse los animales y las plantas.
El abejorro tiene mala vista pero detecta la simetria y la forma regular de las flores sabiendo que siendo simetricas hay más posiblidades de encontrar su alimento.Guardar simetria en los seres vivos se debe a que tienen un A D N más selecto y ordenado; por tanto, las flores con colorido y simetria tienen mayor facilidad para reproducirse porque son más vistosas, y premian mejor en calidad y cantidad de nectar, a los insectos colabaradores, que las selecionan porque lo entienden.
Los virus son simétricos porque es la mejor manera de realizar muchas copias de si mismo con rapidez como él quiere; ser simétricos, es una regla facil para la reprodución; lo dificultoso y lento seria si cada uno fuera irregular y distinto.
El mundo inanimado tambien tiene su simetria, los cristales de los copos de nieve, etc., en las rocas la simetría es muy eficaz, para compactar y dar fuerza; el motivo de que el diamante cristalice en tetraedros es porque es una simetría extremadamente resistente.Conclusión.-
El número de oro, siempre ha estado y estará con nosotros, al igual que Pi siempre ha estado y estará con la circunferencia.
Termino con la conocida frase de que...
LA NATURALEZA ES MUY SABIA.
POR ELLO, EL CONOCIMIENTO DE LA ESTRUCTURA DE SU BELLEZA RESIDE EN ALGO INALTERABLE, LAS MATEMATICAS.
*******************************
Curiosidad.-Solo hay un número en el idioma español que tiene tantas letras como el valor que representa ..... EL CINCO.
Algunas curiosidades de operaciones matemáticas.-
---1x8+1= 9 --------- 1x1= 1----------------1x9+2= 11
-12x8+2 = 98 -------11x11 =121----------12x9+3=111
123x8 +3 = 987 -- 111x111 = 12321--123x9+ 4 = 1111
etc.
*************
-------------9 x 9 + 7 = 88
------------98 x 9 +6 = 888
-----------987 x 9 + 5 = 8888
----------9876 x 9 + 4 = 88888
etc.
CURIOSIDADES MATEMÁTICAS DE LOS NÚMEROS PRIMOS Y DEL AÑO 2.011.-
Los Números Primos.
Todos los números se forman multiplicando los primos entre si, por tanto, los números primos, son los " ladrillos " con los que se construye cualquier número natural.
Los primos son a los números como los átomos a la materia.El número 2.011 es un múmero primo.
Pero....
..... resulta que, ONCE NÚMEROS PRIMOS CONSECUTIVOS sumados dan 2.011
Estos son :
157 + 163 + 167 + 173 + 179 + 181 + 191 + 193 + 197 + 199 + 211 = 2. 011.
***************************
Pincelada final.-Los números y sus leyes, conviven y han convivido con nosotros, desde siempre, y para siempre.LAS MATEMÁTICAS TRASCIENDEN LAS CULTURAS.
LOS NÚMEROS PRIMOS SON, LOS LADRILLOS DEL UNIVERSO.
- Marco du Santoy -
TODO, ESTA REGIDO POR NÚMEROS Y FORMAS MATEMÁTICAS.
- Pitágoras -
****************************
EXTREMADURA.
Verano 2.011
El Duende Euriteño.
